作者投稿
专家审稿
编辑办公
Simulation Study on Railway Track Measurement Based on a Multi-Dimensional Calibration Platform
-
摘要:
轨道几何检测系统在保障高速铁路运行安全与效率方面发挥着关键作用，但复杂的轨道几何状态和动态工况对检测系统的校准精度提出了严峻挑战。设计了一种基于多维振动试验平台的轨道几何检测系统校准试验台，结合运动模拟和数据解算方法，为轨道几何检测系统的校准提供了可靠的测试平台。试验台由车体姿态、转向架姿态、轨道姿态及轨道几何不平顺四个模拟模块组成，结合数字控制与高精度校准装置，可复现复杂工况下的轨道几何状态。实验验证显示，试验台在重复性与一致性方面表现良好。重复性实验中，轨道几何不平顺参数的误差均满足检测限值，左高低、右高低和轨向的重复性误差分别为0.16 mm、0.15 mm和0.31 mm；一致性实验中，试验台复现的短波高低、轨向与轨距数据与现场实测数据高度吻合，短波高低误差为0.46 mm，轨向误差为0.63 mm，轨距误差为0.45 mm。新增的构架姿态测量模块进一步提升了试验台在动态工况下的精度与稳定性。研究结果表明，该校准试验台在复杂动态工况下具有高精度和可靠性，为轨道几何检测系统的优化与高铁运行安全保障提供了重要技术支持。未来将进一步优化数据融合算法与硬件性能，扩展试验台的适用范围。
Abstract:Track geometry measurement systems play a critical role in ensuring the safety and efficiency of high-speed railway operations. However, complex track geometry conditions and dynamic scenarios pose significant challenges to calibration accuracy. To address these challenges, this study proposes a track geometry measurement system calibration platform based on a multi-dimensional vibration test platform. The platform integrates motion simulation and data processing methods to provide a reliable calibration solution. It comprises four simulation modules: car body posture, bogie posture, track posture, and track geometry irregularities. By leveraging digital control systems and high-precision calibration devices, the platform replicates complex track geometry states under dynamic conditions. Experimental results demonstrate excellent performance in terms of repeatability and consistency. In repeatability tests, the errors of reproduced track geometry irregularity parameters meet detection limits, with repeatability errors for left longitudinal level, right longitudinal level, and alignment being 0.16 mm, 0.15 mm, and 0.31 mm, respectively. Consistency tests reveal close alignment between simulated and field-measured data, with short-wave longitudinal level, alignment, and track gauge errors of 0.46 mm, 0.63 mm, and 0.45 mm, respectively. The newly incorporated bogie posture measurement module further enhances the platform’s precision and reliability under dynamic conditions. The findings confirm the platform’s high accuracy and reliability, providing critical support for optimizing track geometry measurement systems and ensuring high-speed railway safety. Future research will focus on refining data fusion algorithms and improving hardware performance to expand the platform’s application range.
-
0. 引言
随着高速铁路的快速发展，轨道几何检测系统在保障铁路运行安全与提高运营效率方面发挥着至关重要的作用。这些系统通过检测轨距、高低、轨向等轨道几何不平顺参数，为基础设施的维护和优化提供了重要依据。然而，由于轨道几何异常的复杂性、列车运行时的动态姿态及设备耦合作用，现有检测系统在实际运行条件下的精度和可靠性仍面临诸多挑战。因此，如何在实验室环境中对轨道几何检测系统进行动态校准测试，成为当前铁路检测领域亟待解决的重要问题。
目前高速列车构架运动状态的分析主要集中于构架振动加速度测量和动力学仿真建模。其中，文献[1 - 2]提出了通过安装在服役车辆上的不同传感器的测量来评估轨道不规则性对构架的影响，并进行了实验验证。文献[3]根据6自由度模拟平台几何结构和参数，利用基于欧拉角的齐次变换矩阵建立了6自由度模拟平台位姿正解非线性数学模型，实现了转向架实际线路运行状态的实验室模拟。文献[4]采用两种不同的算法分析了六自由度振动平台在任意时刻的旋转矩阵，并建立了振动平台位姿的反解方程。文献[5]根据齐次变换矩阵中旋转矩阵的正交特性及牛顿迭代实现了转向架空间姿态模拟平台的运动学正解解算。Khouy等[6]利用蒙特卡罗模拟的仿真模型优化轨道几何检测间隔，并假设退化参数服从对数正态分布。Khosravi等[7]结合递归快速傅里叶变换和相关优化变形，精确校正轨道几何数据误差。车载光学检测法和声学检测法在轨道监测中逐渐得到应用。通过高精度激光传感器采集轨道数据[8 - 9]，但光学检测容易受到环境干扰。车载声学检测法通过车体麦克风识别轨道病害[10 - 12]，但其主要应用于损伤识别，尚未有效反推轨道不平顺。此外，研究者们还通过轨道动力响应反推轮轨平顺性，LI等[13]改进了利用钢轨加速度估算轨道不平顺的方法，一些研究者[14 - 15]则利用声发射监测道岔健康状况。结合光纤光栅技术，文献[16 - 18]等实现了道岔的实时监测与预警。上述研究为列车构架的振动特性分析和构架位姿的实验室模拟奠定了基础。
针对构架运动位姿的测量方法，文献[19]提出了一种基于加速度分离算法的姿态测量方法，并根据此算法实现了基于卡尔曼滤波器的高精度姿态解算。文献[20]针对飞行器在姿态解算时容易受到非重力加速度影响的问题，提出了一种自适应误差四元数无迹卡尔曼滤波的飞行器姿态解算方法。文献[21 - 23]应用 MEMS 陀螺仪和加速度计进行姿态测量，同时利用卡尔曼滤波算法将 MEMS 陀螺仪和加速度计输出的数据进行滤波融合，实现了姿态测量高准确度的要求，实验结果表明应用 MEMS陀螺仪和加速度计的姿态测量精度较高，受外界影响较小，具有良好的可靠性。文献[24]通过在转向架上安装一个惯性测量单元，它可以连续地获取车辆运动的在役数据，并基于列车与轨道的相互作用，使传感器将直接测量到车辆的动态响应，并提取独特的信号特征。文献[25]提出了一种基于车身和转向架加速度测量的轨道状态监测方法，通过安装加速度传感器同时测量垂向和横向加速度。文献[26]设计了两种数据融合算法，以减少 MEMS 传感器的漂移误差和噪声，证明了互补滤波法和最速下降法在数据融合中的有效性。文献[27]提出了一种结合 IMU 和 ODO 的轨道不平顺检测方法，通过卡尔曼滤波融合设计姿态和惯导姿态，并结合里程计速度提高航位推算精度。文献[28]在 GNSS 拒止环境下，采用类似方法显著提升了检测精度和效率。文献[29]提出了一种基于多源车载数据的智能识别方法，通过 PSO 优化的 CNN-LSTM 网络进行轨道不平顺建模和识别，提升了识别精度和效率。文献[30]总结了轨道平顺性检测的研究现状，提出结合数据驱动和模型驱动的方法，利用卡尔曼滤波和深度学习技术实现轨道不平顺检测。上述研究为构架位姿的实时测量和位姿解算提供了指导方法。
尽管国内外在轨道几何测量和姿态模拟领域已取得诸多成果，但仍存在一些亟待解决的问题，包括复杂工况下的姿态估算精度不足，特别是在曲线和道岔等区域，传统方法难以准确捕捉动态姿态变化；实时数据融合与补偿算法的优化需求较为迫切，现有算法在多传感器数据融合的效率和高动态环境下的精度及响应速度方面仍需进一步提升。这些问题的存在制约了相关技术在复杂实际场景中的广泛应用。
针对这一需求，轨道几何检测系统校准试验台为解决轨道几何检测精度问题提供了一种有效的解决方案。通过模拟列车运行中的典型工况，该试验台可以再现车体、转向架及轨道的空间位姿，从而实现对轨道几何检测系统的动态测试校准。试验台由车体姿态模拟子试验台、转向架姿态模拟子试验台、轨道姿态模拟子试验台和轨道几何不平顺模拟子试验台等核心模块组成，采用六自由度运动方式，全面模拟轨道和车辆的动态耦合作用。此外，试验台集成了数字控制系统、激光干涉仪校准系统及校准软件等高精度装置，以保证量值传递的准确性和系统校准的可靠性。
本研究基于实验室条件，通过轨道几何不平顺模拟试验台生成的参考量值与检测系统输出值进行比对分析，完成对轨道几何检测系统的校准工作。通过高精度实验数据的验证，本文设计的校准试验台能够真实再现实际轨道状态和列车运行条件下的复杂动态环境，为轨道检测系统的性能优化提供了科学依据。
本文的创新性在于，首次将车体、转向架及轨道姿态的动态耦合作用引入轨道几何检测系统校准中，通过综合实验平台的高精度控制实现了运动条件下检测系统精度的量化评估与优化。研究结果将为铁路检测系统的进一步发展提供理论支持和技术保障。
1. 轨道检测状态模拟装置与方法
1.1 多维振动试验平台
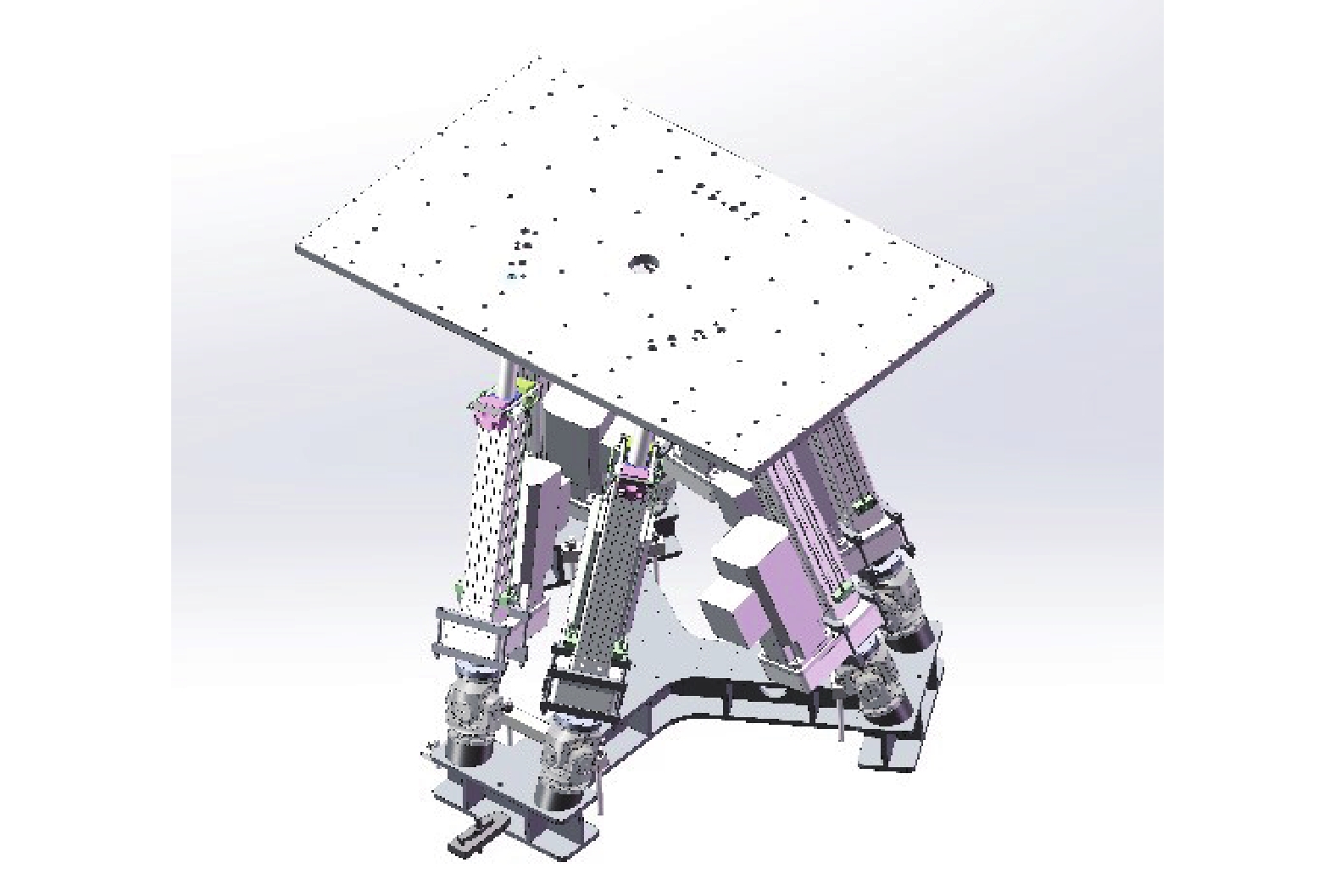
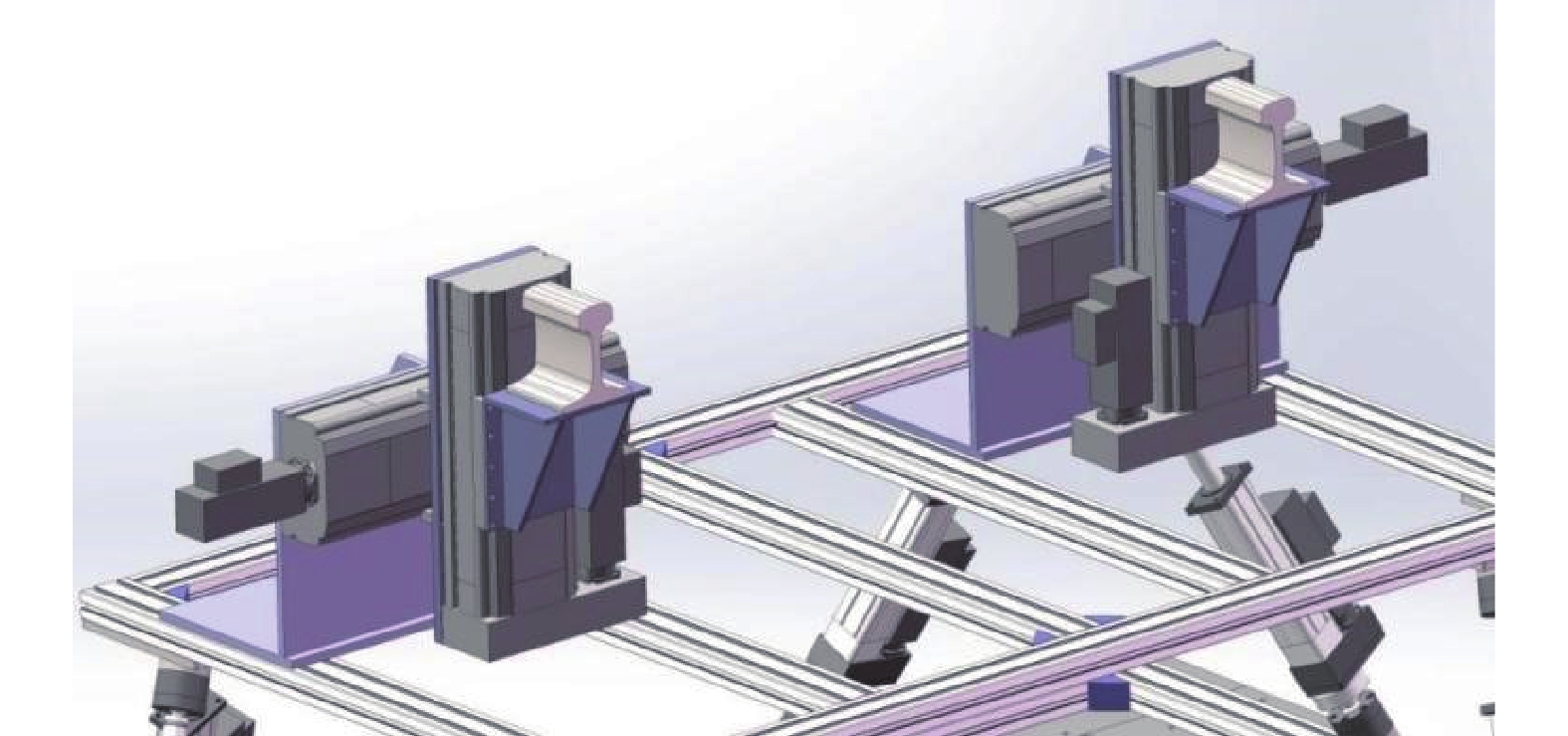
轨道检测状态是指列车运营检测过程中，线路状态与检测系统运动姿态的综合表现。线路状态主要包括轨道的几何不平顺和线路线形变化，其在空间域的表现为左右钢轨沿轨道延伸方向的横向、垂向不平，以及轨道倾角的变化；在时间域的表现为左右钢轨随列车速度变化的横向、垂向位移和轨道平面角度的动态变化。为实现实验室环境下的轨道检测状态复现，本研究设计了一套多维振动试验台系统，通过精确控制多自由度运动模块，模拟车辆和轨道的动态耦合状态，设计如图1所示。
多维振动试验台由四个核心子系统组成，包括车体姿态模拟子试验台、构架姿态模拟子试验台、轨道姿态模拟子试验台及轨道几何不平顺模拟子试验台。这些子试验台协同工作，通过数字控制系统协调运动，可模拟列车和轨道系统在动态条件下的相对姿态。
1.1.1 车体姿态模拟子试验台
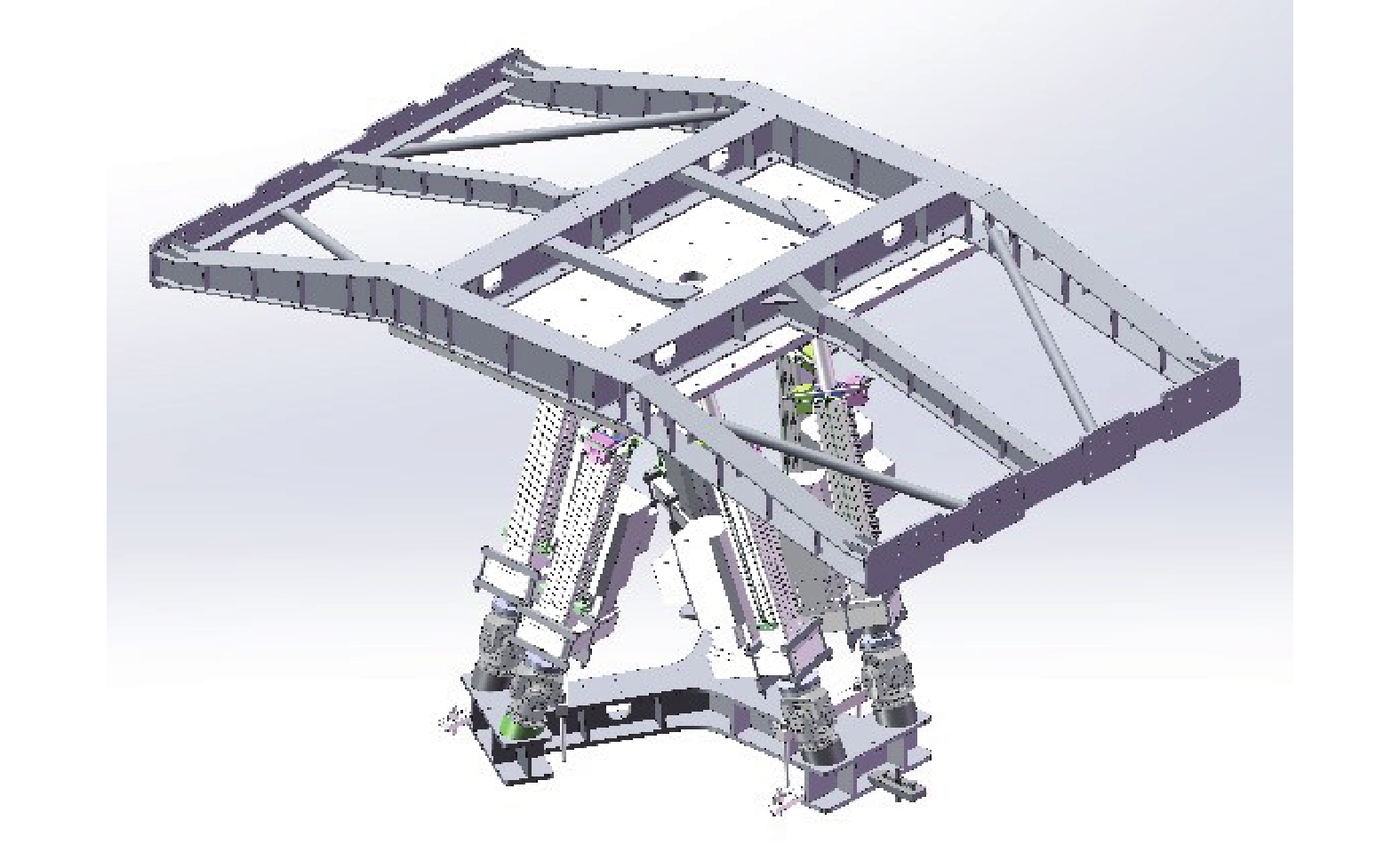
采用六自由度振动试验台，通过独立控制作动器实现3个平移（X、Y、Z）和3个旋转（绕X、Y、Z轴）的运动，全面模拟车体的动态姿态。其底部与转向架姿态模拟子试验台刚性连接。车体姿态模拟子试验台如图2所示。
车体姿态模拟子试验台所采用的电动作动器行程为±120 mm，出力±200 kg，速度750 mm/s，丝杠导程为5 mm；采用的伺服电机参数为转速
9000 转/min，功率2.2 kw，电流6.8A，扭矩2.3 Nm，具有高精度的运动控制能力，可满足多种复杂工况的模拟需求。其设计充分考虑了实验室条件下的动态响应和稳定性，支持单自由度和多自由度的组合运动模式。通过精确控制作动器的位移和速度，该试验台能够复现列车运行过程中车体的典型姿态变化，例如横向位移、垂向位移及绕轴旋转运动。典型工况下，试验台可实现X方向1 Hz加速度1.5 m/s2和Z方向2 Hz加速度2.0 m/s2的动态运动。1.1.2 构架姿态模拟子试验台
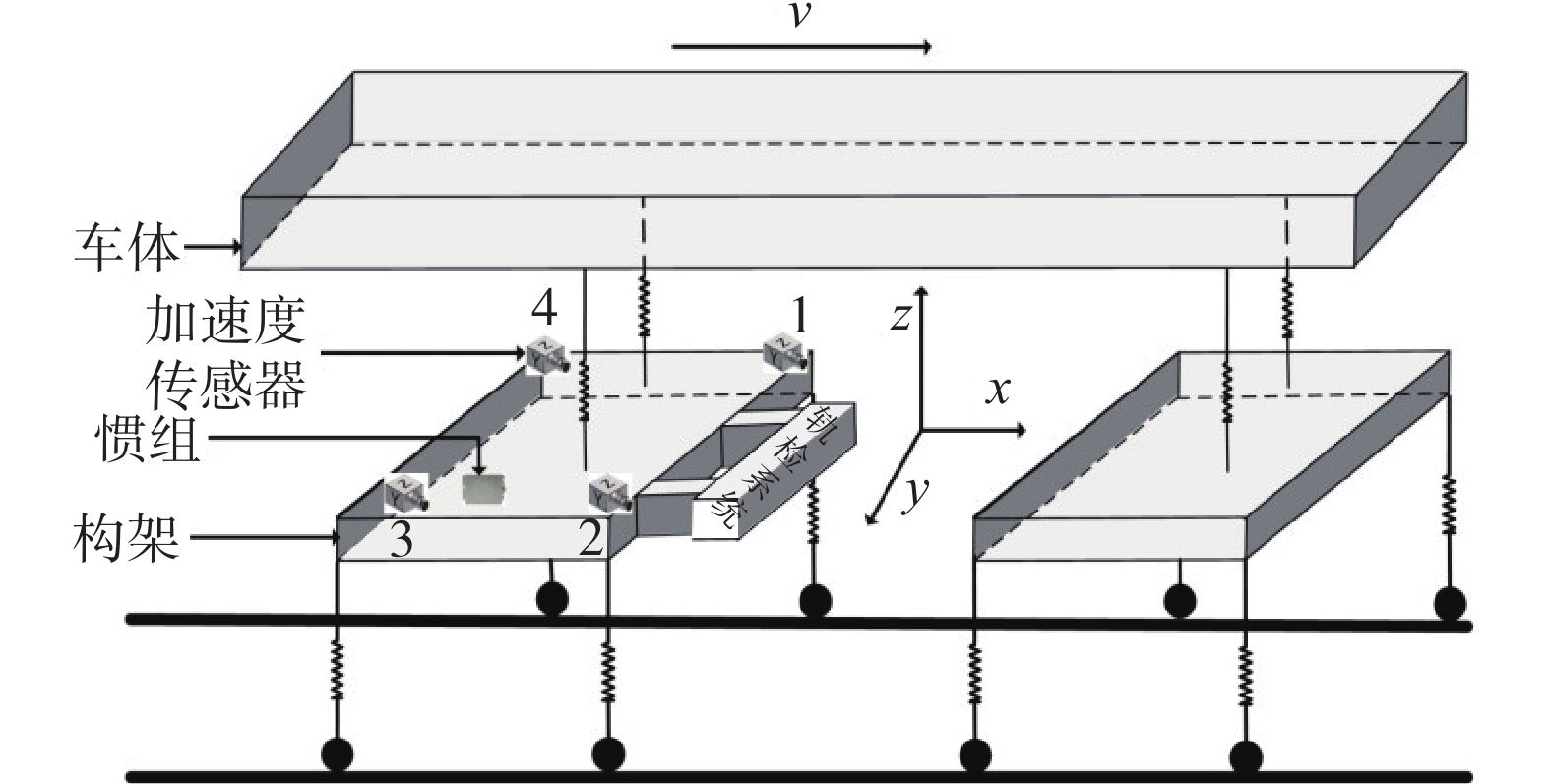
同样为六自由度振动试验台，能够模拟转向架的横向、垂向位移及绕X、Y、Z轴的旋转运动。作为车体姿态模拟子试验台的支撑平台，转向架试验台再现转向架的动态姿态，同时实现车体与构架之间的耦合关系。转向架姿态模拟子试验台如图3所示。为确保构架运动姿态的精准测量，4个三轴加速度计对称安装在被测构架的四个角，惯性组件与第3号加速度传感器安装在同一位置，通过统一的坐标轴方向进行数据采集。其安装位置结合构架几何特点和振动特性设计，能够实现横向、垂向、侧向振动及旋转角的高精度感知，为系统提供基础数据。构架传感器布置如图4所示。
转向架姿态模拟子试验台的电动作动器行程为±250 mm，出力±
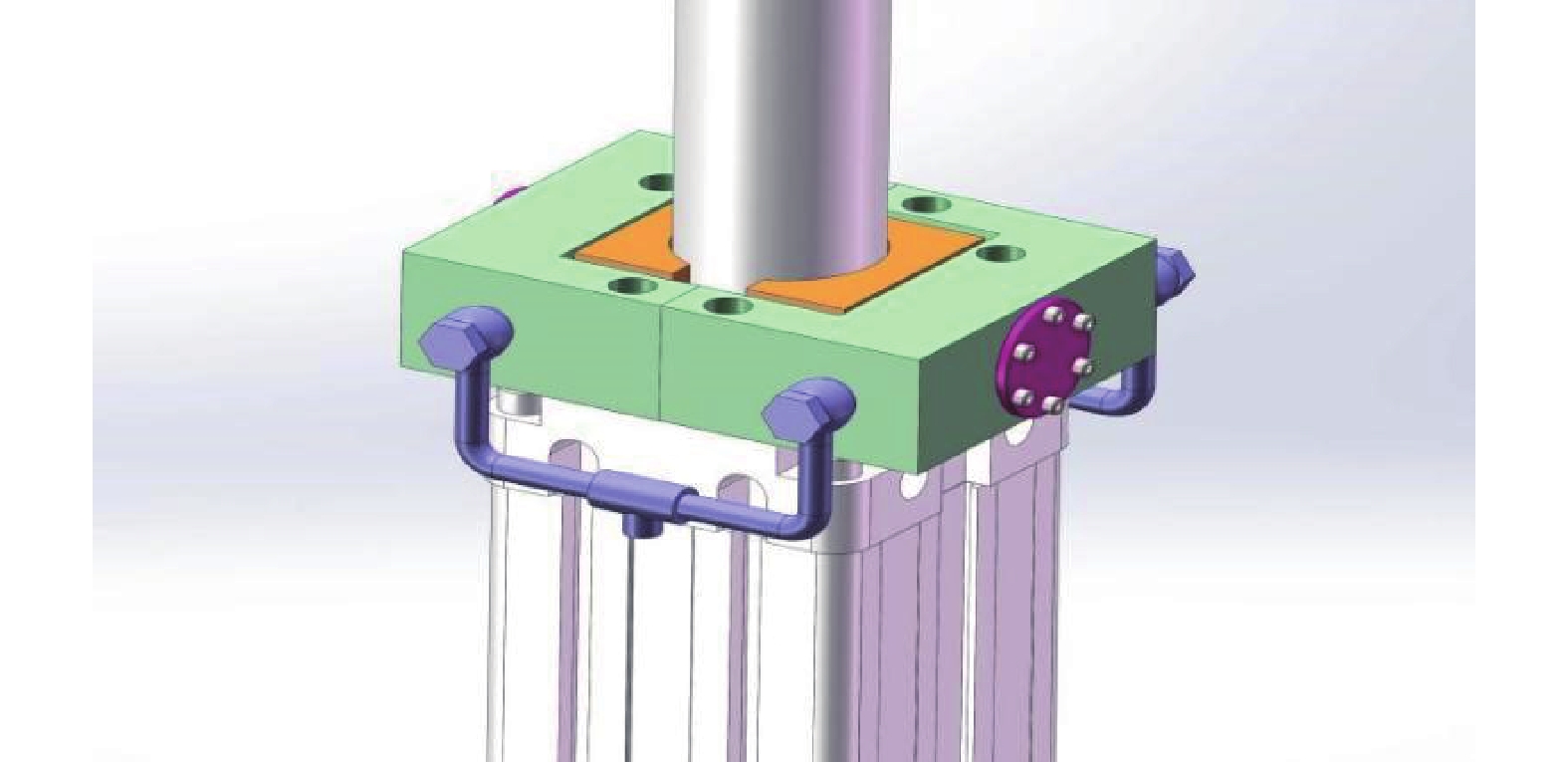
4000 kg，速度750 mm/s，丝杠导程10 mm；伺服电机参数为转速4500 转/min，三相电功率30 kw，电流60A，扭矩90 Nm，总功率为180 KW。转向架姿态模拟子试验台能够在搭载设备质量1200 kg的情况下正常运行，支持0.1 Hz至40 Hz的频率范围，具备X、Y、Z方向最大位移±250 mm和绕X、Y、Z轴最大角度±12°的运动能力。可实现单自由度和多自由度组合运动，并支持多种典型工况，例如0.5 Hz频率下250 mm幅值的X、Z方向振动，或40 Hz频率下0.4 mm幅值的高频振动。为了确保转向架姿态模拟子试验台的安全性，每个作动器上加装了液压式锁紧机构，以应对供电异常等紧急情况，防止试验台发生滑落等事故。液压式锁紧机构的采用可以避免电磁干扰对试验仪器设备和传感器的影响，从而确保试验结果的准确性。液压锁紧机构液压缸示意如图5所示。
1.1.3 轨道模拟子试验台
模拟轨道整体线形的动态变化（如直线到曲线过渡段的倾角变化）。通过多自由度作动器实现对轨道倾角和曲率的精确控制，能够模拟轨道沿长度方向的空间六自由度变化。轨道模拟子试验台的电动作动器行程为±250 mm，出力为±
1200 kg，速度为750 mm/s，其丝杠导程为10 mm；伺服电机参数为转速4500 转/min，三相电功率8.2 kw，电流18A，扭矩26 Nm，总功率50 kW。轨道模拟子试验台如下图所示，采用八作动器方式。该试验台满足X、Y、Z方向最大位移±250 mm，绕X、Y、Z方向最大角度±10°及绕Y轴和Z轴角速度2.0°/s的典型工况。轨道模拟子试验台如图6所示。1.1.4 轨道几何不平顺模拟子试验台
轨道几何不平顺模拟子试验台由两套水平直线模组和垂直振型模组组成，分别用于模拟轨道的横向和垂向运动。可形成不同波长和振幅的轨道几何不平顺参数，并提供轨距、高低和轨向的模拟输入。轨道几何不平顺模拟子试验台水平直线模组行程为±200 mm，垂直直线模组行程为±100 mm，设计出力为±100 kg，速度500 mm/s，丝杠导程10 mm；伺服电机参数为转速
3000 转/min，功率1.9 kw，电流4.3A，扭矩6 Nm。可满足X、Z方向频率10 Hz、幅值5 mm和频率5 Hz、幅值8mm的试验工况，轨道几何不平顺模拟子试验台设计如图7所示。1.2 轨道检测状态模拟软件设计
为了实现轨道几何检测系统校准试验台各子系统的精确控制，本文设计了一套基于上位机和下位机架构的姿态模拟软件系统。该系统采用模块化设计，通过分层结构实现对子系统的同步与异步控制，从而保证了各模块之间的协调工作和数据传输的稳定性。软件系统的设计确保了轨道几何检测系统在复杂动态工况下的高效性和精度。
1.2.1 软件系统架构
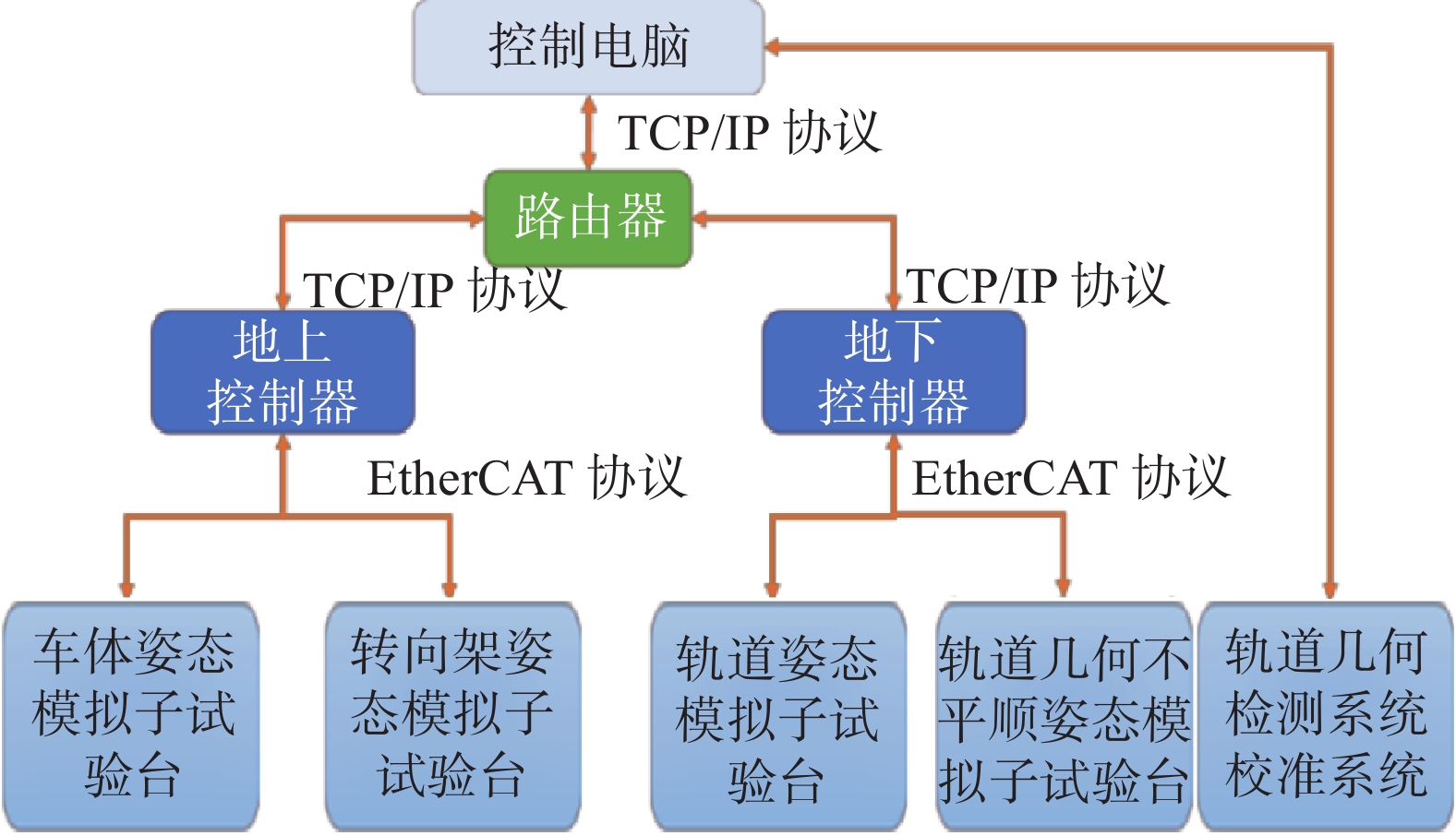
轨道几何检测系统校准试验台的控制系统软件主要分为三部分，分别为：车体姿态模拟子试验台和转向架姿态模拟子试验台控制软件、轨道姿态模拟子试验台和轨道几何不平顺姿态模拟子试验台控制软件、台阵同步控制软件。姿态模拟软件系统架构如图8所示。这三部分软件通过网络通讯进行集成，确保各子系统之间的数据传输与协同控制。通过路由器将各子系统连接在一起，控制电脑与路由器之间的网络连接，使得系统能够实现对子系统的同步与异步控制。
1.2.2 上位机与下位机设计
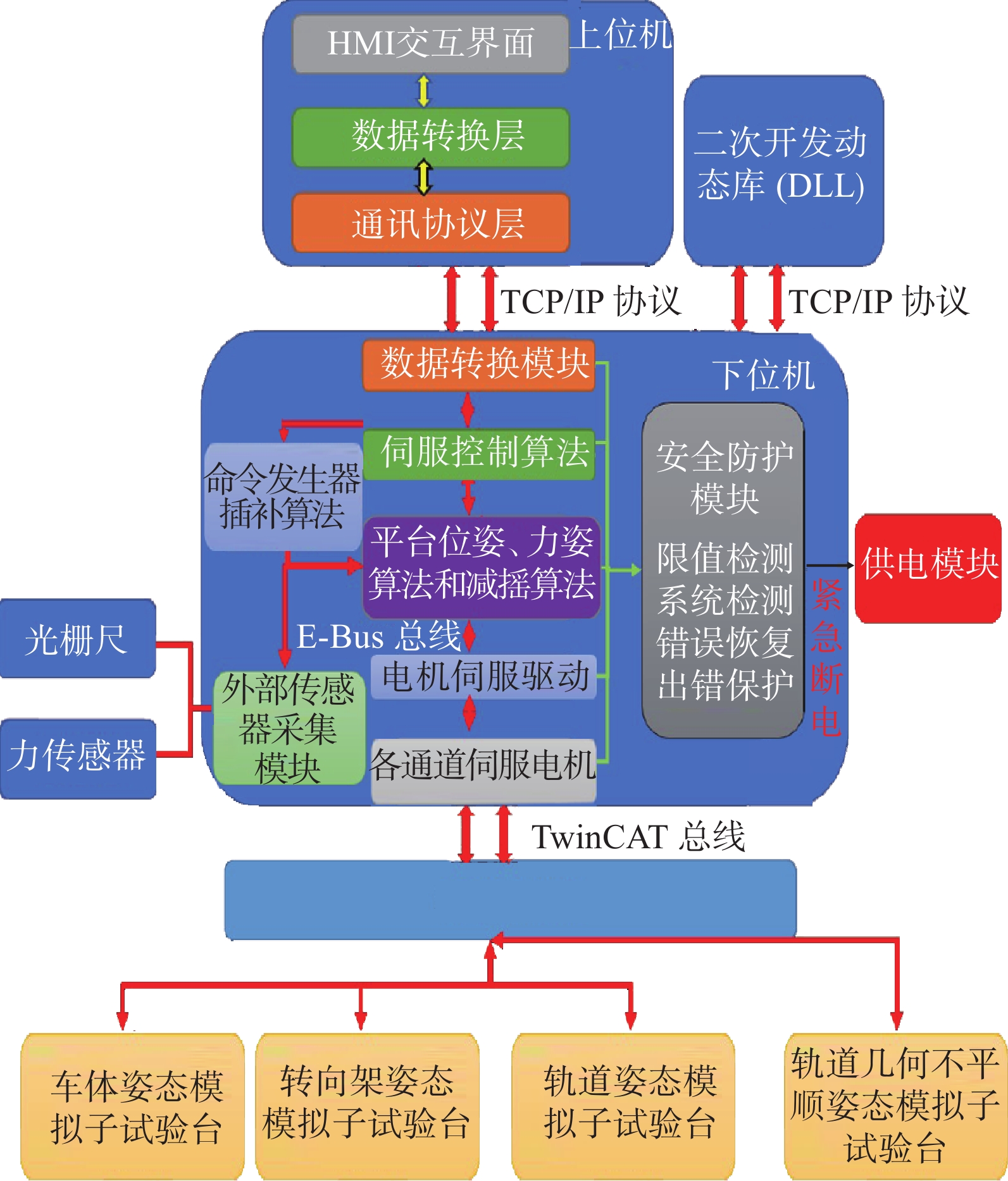
本系统采用上位机与下位机架构进行设计。上位机主要运行在控制电脑端，负责命令的输入、实时数据的显示、以及系统状态的监控。下位机则负责执行具体的平台控制任务，包括平台算法的执行、多自由度解耦、命令插补、伺服运动控制以及数据采集等。上位机与下位机通过TCP/IP协议进行通讯，确保数据传输的实时性与准确性。姿态模拟软件系统上下位机设计如图9所示。
![]()
图 9 姿态模拟软件系统上下位机设计Figure 9. Design of the upper and lower computer architecture for the posture simulation software system上位机的功能模块包括：
1）HMI交互界面：实时显示系统的状态信息，包括位姿姿态、作动器位置等，提供错误报警与限值警告功能，确保用户可以及时发现并处理问题。同时，用户可通过命令设置界面设定平台的运行模式（如位移模式、加速度模式等），并检查输入参数是否超过系统限值；
2）数据转换模块：将下位机上传的数据转化为上位机可识别的格式，保证数据的有效性；
3）网络通讯模块：负责建立与下位机的TCP通讯连接，将加密的数据发送至下位机，并接收下位机上传的数据。
下位机的主要功能模块包括：
1）网络通讯模块：下位机作为服务器端，接收上位机的连接请求并进行数据交换；
2）数据转换模块：将从上位机接收到的数据转化为下位机可识别的格式，并进行数据检验，去除无效或异常数据；
3）命令发生器：生成控制信号，并进行6自由度的自动解耦，确保系统能够处理复杂的动态工况；
4）外部传感器采集模块：负责采集位移传感器、力传感器、加速度传感器等传感器数据，并通过eBus总线将数据传输至控制器；
5）平台位姿与力姿态算法模块：集成六自由度平台位姿逆解与正解算法、力姿态解算算法以及减摇算法，提供精确的位姿与力学分析；
6）安全防护模块：实时监控系统状态，检测命令与反馈值是否超限，一旦发生超限或错误，系统会自动进行错误恢复或重启，确保设备安全运行；
7）伺服控制算法模块：将系统设定的命令值转化为伺服系统可以识别的信号，结合PID控制和滤波算法来优化伺服机构的精度与响应速度；
8）电机伺服驱动模块：将数字量信号转化为电信号，用于驱动电机执行平台运动。
1.2.3 系统通信与协调
确保各部分子系统能够高效协同工作，系统采用基于TCP/IP协议的网络通讯方式，实现了上下位机之间的数据实时交换。下位机作为服务器端，持续监控并接收上位机发出的控制信号，在实时执行平台控制任务的同时，保证了数据的稳定传输和指令的及时响应。此外，系统设计还确保了数据传输过程中的安全性与可靠性。
2. 姿态结算与数据处理
在轨道几何检测系统的动态校准过程中，精确获取构架的姿态信息是至关重要的。由于多维振动试验平台模拟的工况复杂且涉及高频与低频振动响应，单纯依赖传统的传感器数据可能无法满足高精度要求，因此，本研究设计了一套高效的姿态解算与数据处理算法，以便从加速度计等传感器采集的原始数据中准确地解算出列车构架的动态姿态。
2.1 频域积分与低频衰减算法
在轨道几何检测系统中，传感器采集的加速度信号通常受环境噪声、传感器漂移及低频干扰等因素影响，直接影响姿态解算的准确性。为确保位移数据的可靠性，本文采用频域积分方法对加速度信号进行处理。首先，通过对加速度信号进行傅里叶变换（FFT），将其从时域转换为频域进行分析，进而通过频域积分计算出位移数据。具体而言，通过离散傅里叶变换（DFT）代替传统的积分过程，从而有效避免误差的累积和放大。
A(f)=∫a(t)⋅e−i2πftdt (1) 在此基础上，得到的频域信号A(f)可以通过傅里叶逆变换转换回时域，以获得准确的位移数据。
x(t)=∫A(t)⋅ei2πftdf (2) 然而，在实际应用中，低频噪声通常会对加速度信号产生较大干扰，尤其是在轨道几何不平顺、设备漂移等情况下。为此，本研究引入了低频衰减方法，采用高通滤波器来去除低频噪声并保留有效信号。该滤波器通过设置目标频率f0和精度系数α，可以在确保不丢失有效信号的前提下有效衰减低频噪声。
Target(f)=ff+α (3) 这一技术能够有效降低低频信号对姿态解算的干扰，同时最大限度保留目标频段的有效数据，从而提高位移解算的精度。
2.2 数据融合与卡尔曼滤波
在复杂的轨道工况下，单一的加速度计数据难以满足精确的姿态解算需求，因此，本研究设计了一种基于惯性测量单元（IMU）和加速度计数据融合的解算算法。IMU数据能够提供低频的稳定姿态信息，而加速度计则能够提供高频的动态响应信息。为了优化解算过程，减少测量误差和传感器漂移，采用了卡尔曼滤波算法。具体而言，卡尔曼滤波算法能够对加速度计和IMU输出的数据进行动态估计和误差修正，从而提高数据的准确性和可靠性。卡尔曼滤波的基本过程可通过以下递推公式进行表述。
ˆx(k|k)=ˆx(k|k−1)+Kk[z(k)−Hˆx(k|k−1)] (4) 式中，ˆx(k|k)表示当前时刻的估计值；z(k)为当前测量值，Kk为卡尔曼增益；H是测量矩阵，表示观测模型。通过卡尔曼滤波，系统能够有效融合来自加速度计和惯性测量单元的数据，实时补偿传感器的误差，特别是针对动态环境中的轨道几何不平顺等因素，卡尔曼滤波不仅优化了姿态估算，还提高了测量数据的实时性和精度。
2.3 姿态解算过程
在列车动态运行的复杂环境中，传感器的安装误差和动态响应非线性因素都会对姿态解算结果产生影响。因此，本研究通过旋转矩阵和坐标变换的方法，精确计算构架的位移与转角。设定惯性坐标系和随体坐标系，并通过旋转矩阵实现二者之间的坐标转换，从而获得准确的构架运动状态。具体而言，侧滚角和摇头角的计算方法如下。
2.3.1 测点位移解算
通过测量点i处的加速度数据ai(t) 和相应的频域积分计算出每个测点的位移数据di(t)，将多个测点的数据结合后，通过坐标转换技术，解算出构架几何中心的横向位移dx(t)和垂向位移dz(t)。
dx(t)=144∑i=1di,x(t) (5) dz(t)=144∑i=1di,z(t) (6) 这些位移数据反映了构架的基本运动情况，并为后续的姿态角计算提供了基础。
2.3.2 姿态角解算
利用构架上不同测点的位移数据，通过几何关系计算得到构架的侧滚角θx和摇头角θz具体计算公式如下。
θx=arctan(d1,y−d3,yd1,z−d3,z) (7) θz=arctan(d2,y−d4,yd12x−d4,x) (8) 式中，di,y为测点的纵向位移。
通过将上述算法与轨道几何检测系统的姿态模拟平台相结合，能够在实验室环境下模拟复杂轨道工况，验证解算算法的准确性与鲁棒性。特别是在复杂的轨道条件下，频域积分和低频衰减技术有效过滤了无效信号，卡尔曼滤波算法进一步提高了系统的精度和实时响应能力，为轨道几何检测系统的精确校准提供了有力支持。
3. 轨道检测状态模拟试验验证
本节将通过实验数据对系统的性能进行验证，重点分析轨道几何检测系统在实验室环境中的复现精度及其与现场实际工况的吻合程度。实验主要通过将构架姿态数据与轨道几何不平顺数据导入到试验台，模拟车辆与轨道在动态工况下的行为，评估系统的重复性与一致性。
3.1 实验设置与数据导入
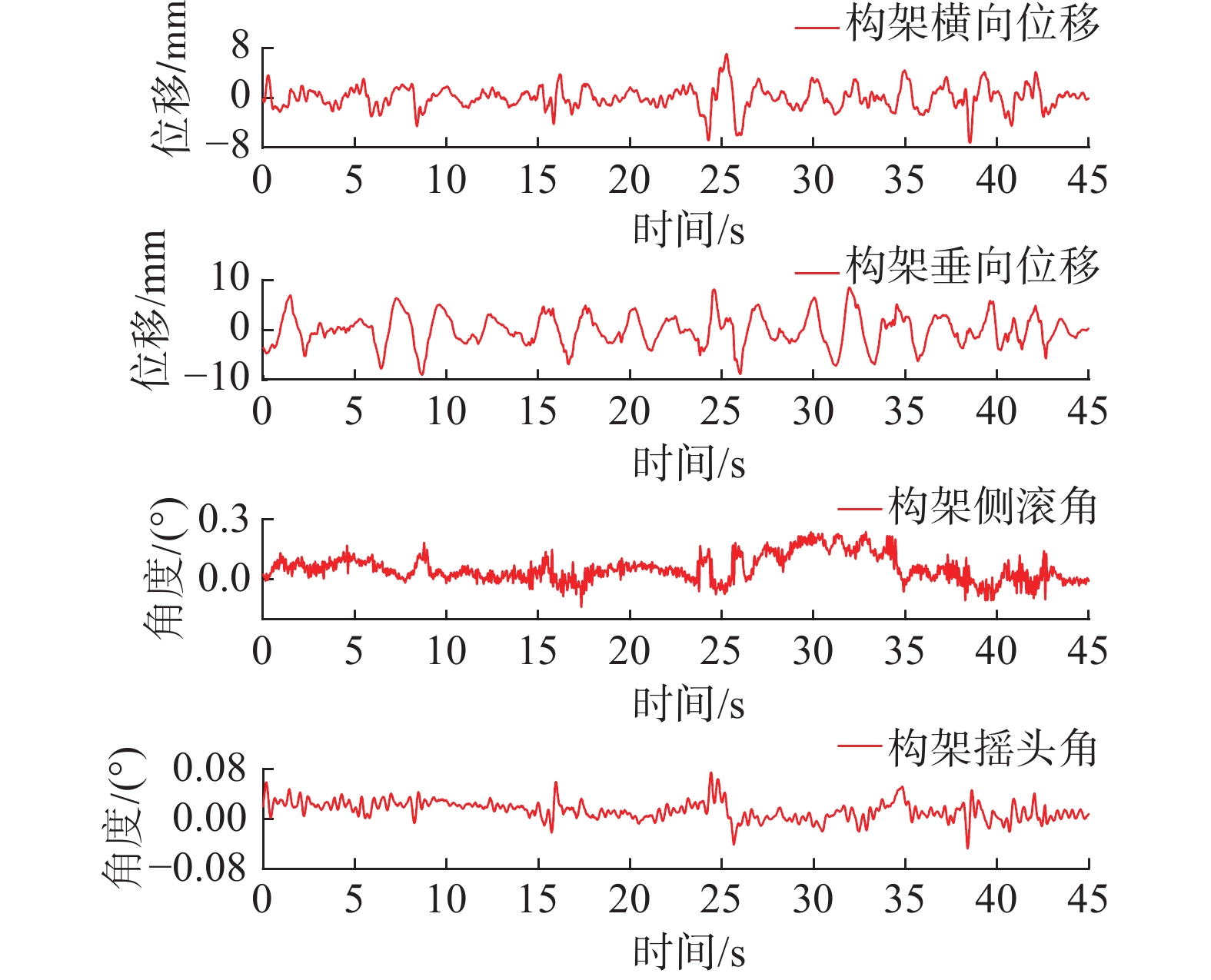
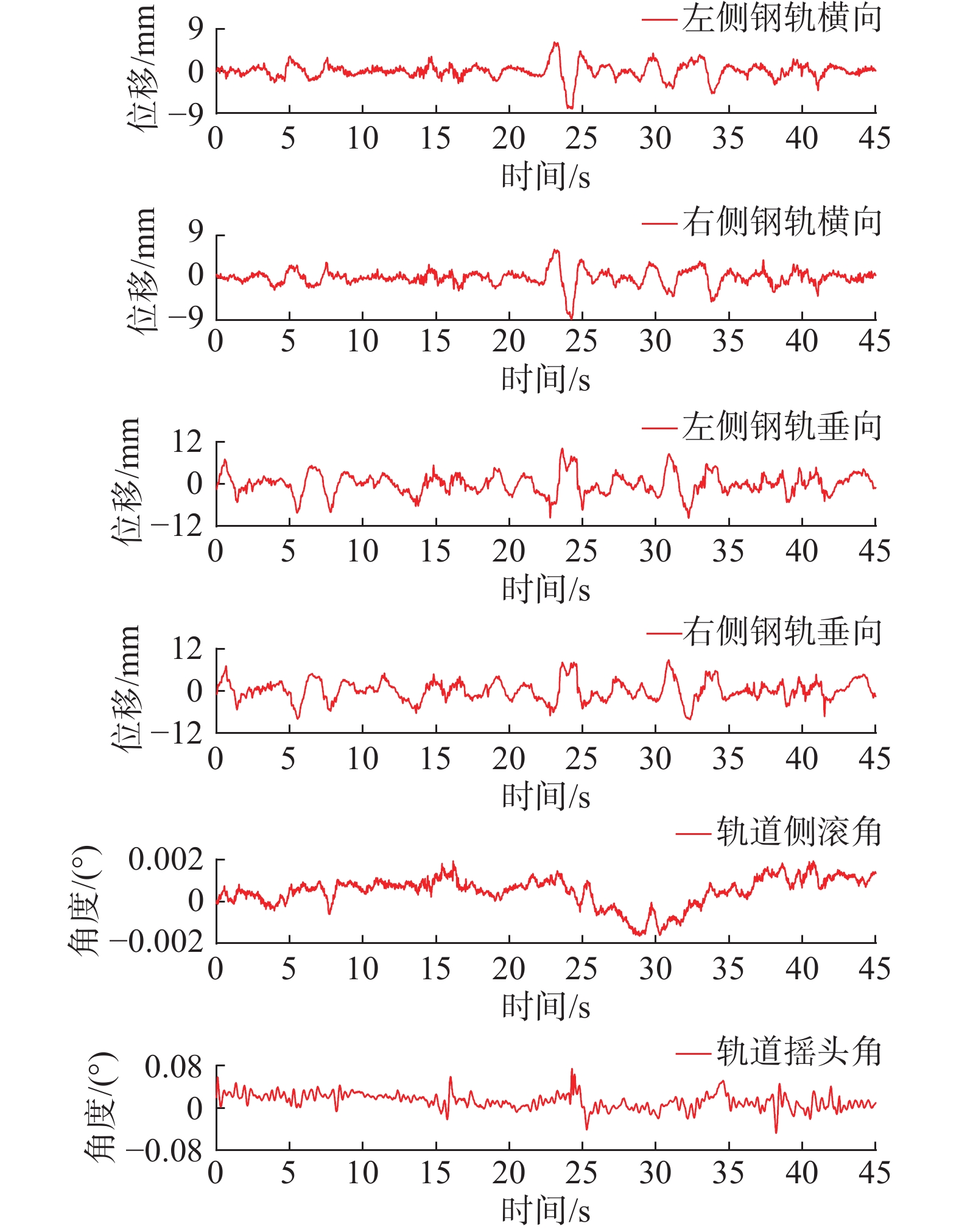
本实验选取高速综合检测列车0501在徐兰高速铁路上的一段相同里程为实验样本。实验使用构架姿态采集系统获取了实际线路中车辆的构架中心姿态数据，使用轨道几何检测系统获取了轨道几何不平顺数据。在实验室中，轨道几何检测系统校准试验台被用于复现这些数据。通过分析与解耦构架姿态数据和轨道几何不平顺数据，分别将其导入轨检系统校准试验台进行模拟复现。构架姿态模拟子试验台和轨道姿态模拟子试验台所导入的数据如图10和图11所示。
![]()
图 10 构架姿态模拟子试验台导入数据Figure 10. Imported data for the bogie posture simulation sub-test platform![]()
图 11 轨道姿态模拟子试验台导入数据Figure 11. Imported data for the track posture simulation sub-test platform试验过程中，轨道几何检测系统被搭载于构架姿态模拟子试验台上，测量并分析轨道的不平顺变化。在此过程中，试验台复现轨道几何不平顺结果的重复性和一致性被重点评估。
3.2 重复性分析试验
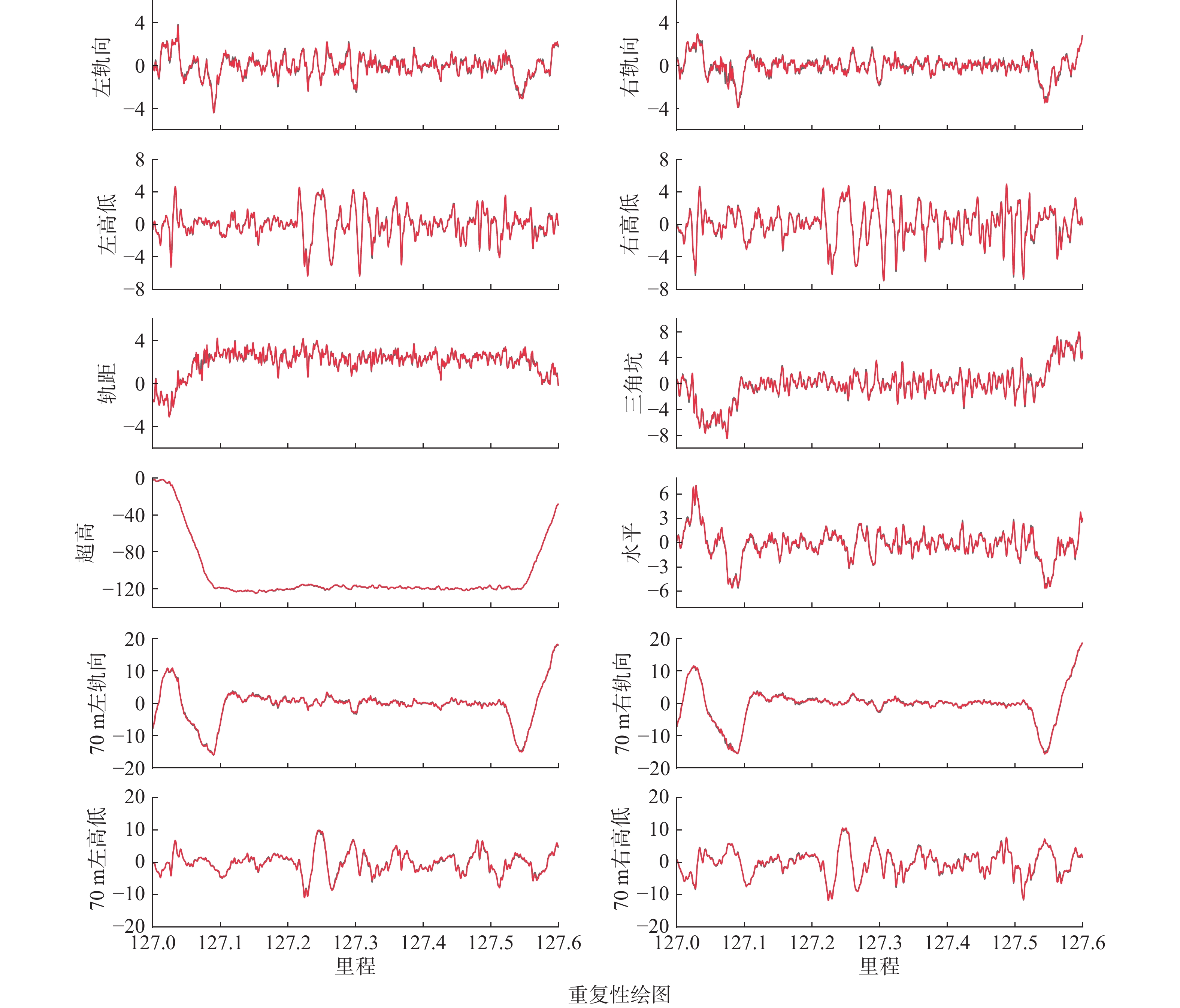
为了评估轨道几何检测系统在相同实验条件下的测量重复性，进行了两次相同里程的车辆和轨道同步复现实验。图12展示了两次模拟试验的轨道几何检测结果。从结果可以看出，两次模拟试验的轨道几何检测系统测量波形具有良好的趋势一致性，证明试验台能够稳定复现轨道几何不平顺数据。
![]()
图 12 模拟轨道不平顺与现场测量重复性试验比对图Figure 12. Comparison of simulated track irregularities and on-site measurements in repeatability tests为进一步定量评估两次试验的重复性差异，本研究引入了误差评价指标，并选取两次实验结果差异的第95%分位数作为重复性误差分析的标准。剔除了粗大误差、外界干扰等因素的影响，得到了重复性验证实验的结果，具体如表1所示。
表 1 模拟轨道几何不平顺重复性测量结果Table 1. Repeatability measurement results of simulated track geometry irregularities序号 项目 差异的第95%分位数 重复性评定指标 1 左高低 0.16 mm 0.6 mm 2 右高低 0.15 mm 0.6 mm 3 左轨向 0.31 mm 0.5 mm 4 右轨向 0.31 mm 0.5 mm 5 轨距 0.12 mm 0.5 mm 6 水平 0.22 mm 0.5 mm 7 三角坑 0.31 mm 0.6 mm 8 70 m左高低 0.14 mm 1.0 mm 9 70 m右高低 0.13 mm 1.0 mm 10 70 m左轨向 0.31 mm 0.8 mm 11 70 m右轨向 0.32 mm 0.8 mm 表中数据表明，两次模拟试验的轨道几何不平顺重复性测量结果满足轨道几何检测系统的重复性限值要求，表明所设计的轨道几何检测系统校准试验台具有较好的重复性
3.3 一致性分析试验
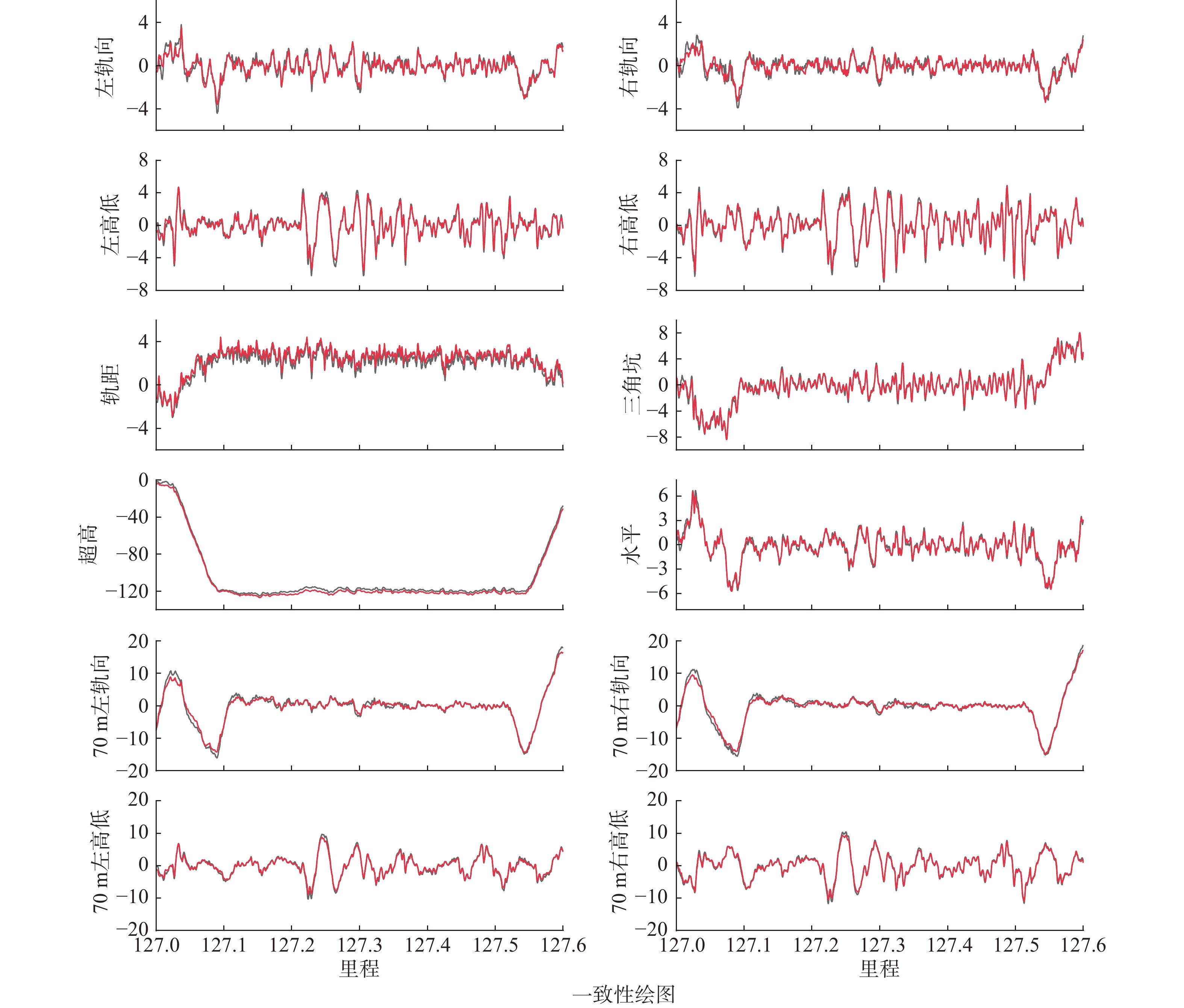
为了进一步验证实验室模拟结果与现场实际工况的吻合度，本实验将试验台模拟条件下测得的轨道几何不平顺数据与现场采集的轨道几何不平顺数据进行了对比。
图13展示了实验室模拟轨道不平顺与现场测量一致性结果的比对。结果表明，实验室模拟数据与现场工况数据在短波高低、轨向、水平、三角坑等参数上具有较好的一致性，证明了实验室姿态同步模拟方法的可行性。然而，针对轨距的复现结果，由于试验台通过导入左、右长波轨向数据来驱动左右钢轨形成轨距，而非单边轨距GL、GR，轨向数据的滤波会导致高频成分丢失，因此轨距复现结果与现场测量结果存在一定差异。该差异是由所用驱动数据造成的，是合理的误差。
![]()
图 13 模拟轨道不平顺与现场测量一致性结果比对图Figure 13. Comparison diagram of simulated track irregularities and on-site measurement results此外，轨道几何检测系统在高低、轨向等参数的测量中具有滤波特性，这会对测量结果产生一定影响。特别是在使用70米长波数据作为试验台驱动数据时，轨道几何检测系统能够较准确地测量短波高低、轨向等数据，但对于70米长波数据，二次滤波会导致幅值差异。因此，在轨道几何不平顺数据的实验室复现中，尽可能选取长波数据以提高复现的准确性。
表2列出了实验室模拟轨道不平顺数据与现场测量数据的一致性分析结果。根据表中的数据，短波高低、轨向、水平、三角坑等参数的差异较小，而对于轨距、长波高低和轨向等参数则存在较大的差异。实验结果与理论预期一致，证明了轨道几何检测系统校准试验台能够有效复现轨道几何不平顺状态。
表 2 模拟轨道不平顺与现场测量结果一致性Table 2. Consistency between simulated track irregularities and on-site measurement results序号 项目 差异的第95%分位数 1 左高低 0.46 mm 2 右高低 0.43 mm 3 左轨向 0.63 mm 4 右轨向 0.77 mm 5 轨距 0.45 mm 6 水平 0.43 mm 7 三角坑 0.84 mm 8 70 m左高低 1.05 mm 9 70 m右高低 1.15 mm 10 70 m左轨向 0.94 mm 11 70 m右轨向 0.95 mm 通过上述实验验证，本研究所设计的轨道几何检测系统校准试验台能够有效复现实际工况下的轨道几何不平顺数据，并在重复性和一致性上都表现出了良好的性能。实验结果表明，实验室模拟数据与现场工况数据在多个参数上具有较好的吻合度，为轨道几何检测系统的性能优化和精度评定提供了可靠的实验依据。进一步的优化可通过选择合适的驱动数据和滤波方式，提高轨道几何不平顺复现的精度和一致性，从而更好地满足轨道几何检测系统校准的需求。
4. 结论
本文设计并实现了一套基于多维振动试验平台的轨道几何检测系统校准试验台，通过六自由度运动模拟列车与轨道的动态耦合作用，复现了复杂工况下轨道几何不平顺及车辆动态姿态。试验台集成了车体姿态、转向架姿态、轨道姿态及轨道几何不平顺四个模块，基于加速度计和惯性测量组件的数据采集与姿态解算技术，能够精确测量构架的横向、垂向位移及姿态角（侧滚角和摇头角），大幅提升了试验台在复杂工况下的精度和可靠性。
通过实验验证，轨道几何检测系统校准试验台在重复性和一致性方面表现出良好的性能。重复性实验中，轨道几何不平顺关键参数的误差均满足检测限值，左高低、右高低和轨向的重复性误差分别为0.16 mm、0.15 mm和0.31 mm。一致性实验结果表明，实验室模拟数据与现场实测数据在短波高低、轨向等参数上的吻合度较高，短波高低误差为0.46 mm，轨向误差为0.63 mm，轨距误差为0.45 mm。实验结果验证了该校准试验台的高精度和可靠性，为高铁运行的安全与效率保障提供了重要的理论支持与技术依据，同时为后续研究奠定了良好的基础。
尽管试验台在复杂工况模拟和系统校准方面取得了显著成果，但仍存在一些不足之处：1) 针对轨距复现精度较低的问题，因数据滤波导致高频成分丢失，需优化轨向驱动数据及滤波算法以提高轨距复现的准确性；2) 在70米长波轨道几何参数模拟中，由于二次滤波对幅值的影响，长波高低和轨向参数的误差略大，需通过改进数据处理算法和硬件性能以降低误差。
本研究的未来展望包括以下几个方向：
1) 扩展试验台在更多样化动态工况（如极端条件、曲线段和道岔区域）的适用性，全面提升轨道几何检测系统在复杂环境下的精度；
2) 深化多传感器数据融合技术研究，优化动态补偿与滤波算法，以进一步提高系统的实时响应能力和复现精度；
3) 探索人工智能与深度学习技术在轨道几何不平顺状态建模与识别中的应用，实现对轨道状态更高效、更智能的分析与评估。
-
![]()
图 9 姿态模拟软件系统上下位机设计
Figure 9. Design of the upper and lower computer architecture for the posture simulation software system
![]()
图 10 构架姿态模拟子试验台导入数据
Figure 10. Imported data for the bogie posture simulation sub-test platform
![]()
图 11 轨道姿态模拟子试验台导入数据
Figure 11. Imported data for the track posture simulation sub-test platform
![]()
图 12 模拟轨道不平顺与现场测量重复性试验比对图
Figure 12. Comparison of simulated track irregularities and on-site measurements in repeatability tests
![]()
图 13 模拟轨道不平顺与现场测量一致性结果比对图
Figure 13. Comparison diagram of simulated track irregularities and on-site measurement results
表 1 模拟轨道几何不平顺重复性测量结果
Table 1 Repeatability measurement results of simulated track geometry irregularities
序号 项目 差异的第95%分位数 重复性评定指标 1 左高低 0.16 mm 0.6 mm 2 右高低 0.15 mm 0.6 mm 3 左轨向 0.31 mm 0.5 mm 4 右轨向 0.31 mm 0.5 mm 5 轨距 0.12 mm 0.5 mm 6 水平 0.22 mm 0.5 mm 7 三角坑 0.31 mm 0.6 mm 8 70 m左高低 0.14 mm 1.0 mm 9 70 m右高低 0.13 mm 1.0 mm 10 70 m左轨向 0.31 mm 0.8 mm 11 70 m右轨向 0.32 mm 0.8 mm 
下载: 导出CSV
表 2 模拟轨道不平顺与现场测量结果一致性
Table 2 Consistency between simulated track irregularities and on-site measurement results
序号 项目 差异的第95%分位数 1 左高低 0.46 mm 2 右高低 0.43 mm 3 左轨向 0.63 mm 4 右轨向 0.77 mm 5 轨距 0.45 mm 6 水平 0.43 mm 7 三角坑 0.84 mm 8 70 m左高低 1.05 mm 9 70 m右高低 1.15 mm 10 70 m左轨向 0.94 mm 11 70 m右轨向 0.95 mm
下载: 导出CSV
-
[1] S. Muñoz, P. Urda, J. L. Escalona. Experimental measurement of track irregularities using a scaled track recording vehicle and Kalman filtering techniques[J]. Mechanical Systems and Signal Processing, 2022, 169: 108625.
[2] S. Muñoz, J. Ros P. Urda, J. L. Escalona. Estimation of lateral track irregularity using a Kalman filter. Experimental validation[J]. Journal of Sound and Vibration, 2021, 504: 116122.
[3] 刘玉梅, 曹晓宁, 苏建, 等. 转向架测试6自由度模拟平台位姿正解解算[J]. 江苏大学学报, 2012, 33(6): 621-626. [4] 林文强, 卢均山, 周生浩, 等. 六自由度振动平台的位姿解算与路谱模拟分析[J]. 机床与液压, 2017, 45(15): 109-113. DOI: 10.3969/j.issn.1001-3881.2017.15.028 [5] 王秀刚, 苏建, 曹晓宁, 等. 基于旋转矩阵正交性的转向架6自由度平台位姿正解解算[J]. 吉林大学学报(工学版), 2013, 43(5): 1241-1247. [6] Khouy I A, Larsson-Kråik P O, Nissen A, et al. Optimisation of track geometry inspection interval[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2014, 228(5): 546-556. DOI: 10.1177/0954409713484711
[7] Khosravi M, Soleimanmeigouni I, Ahmadi A, et al. Reducing the positional errors of railway track geometry measurements using alignment methods: A comparative case study[J]. Measurement, 2021, 178: 109383. DOI: 10.1016/j.measurement.2021.109383
[8] 李海龙. 基于ARM的非接触式轨道检测系统设计[D]. 成都: 西南交通大学, 2017. [9] 尹代洲, 张金红, 彭登全. 轨道平顺性检测方法研究[J]. 测控技术, 2016, 35(11): 119-122. DOI: 10.3969/j.issn.1000-8829.2016.11.030 [10] Mori H , Tsunashima H , Kojima T , et al. Condition Monitoring of Railway Track Using In-service Vehicle[J]. Journal of Mechanical Systems for Transportation and Logistics, 2010, 3: 154-165.
[11] Wang Y, Wang P, Wang Q, et al. Using Vehicle Interior Noise Classification for Monitoring Urban Rail Transit Infrastructure[J]. Sensors, 2020, 20(4): 1112. DOI: 10.3390/s20041112
[12] MA Qinglu, FU Binglin, MA Lian, et al. A Method for Detecting Traffic Accidents on Highway Tunnel Sections Based on Abnormal Sound[J]. Journal of Transport Information and Safety, 2023, 41(1): 34-42.
[13] Li Q, Thompson DJ, Toward MG. Estimation of track parameters and wheel–rail combined roughness from rail vibration[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(4): 1149-1167. DOI: 10.1177/0954409717710126
[14] Junfang Wang, Xiao-Zhou Liu, Yi-Qing Ni. A Bayesian Probabilistic Approach for Acoustic Emission-Based Rail Condition Assessment. Comput[J]. Aided Civ. Infrastruct. Eng, 2018, 33(1): 21-34. DOI: 10.1111/mice.12316
[15] Suwansin W, Phasukkit P. Deep Learning-Based Acoustic Emission Scheme for Nondestructive Localization of Cracks in Train Rails under a Load[J]. Sensors, 2021, 21(1): 272. DOI: 10.3390/s21010272
[16] Cai X, Chang W, Gao L, et al. Design and application of real-time monitoring system for service status of continuously welded turnout on the high-speed railway bridge[J]. Journal of Transportation Safety & Security, 2019, 13(7): 735-758.
[17] Wang Q A, Ni Y Q. Measurement and Forecasting of High-Speed Rail Track Slab Deformation under Uncertain SHM Data Using Variational Heteroscedastic Gaussian Process[J]. Sensors, 2019, 19(15): 3311. DOI: 10.3390/s19153311
[18] Liu X Z, Xu C, Ni Y Q. Wayside Detection of Wheel Minor Defects in High-Speed Trains by a Bayesian Blind Source Separation Method[J]. Sensors, 2019, 19(18): 3981. DOI: 10.3390/s19183981
[19] 王向军, 张朝阳, 刘 峰. 基于加速度分离算法的姿态测量方法研究[J]. 传感技术学报, 2018, 31(12): 1848-1853. [20] 崔培林, 周翟和, 吕品, 等. 自适应误差四元数无迹卡尔曼滤波四旋翼飞行器姿态解算方法[J]. 西安交通大学学报, 2019, 53(3): 97-104. [21] 曹景伟, 朱宝全. 应用 MEMS 陀螺仪和加速度计的汽车运动姿态测量[J]. 重庆理工大学学报(自然科学), 2018, 32(4): 48-55. [22] 徐瑞超, 常丽园. 基于三轴加速度计的姿态测量系统设计[J]. 东莞理工学院学报, 2019, 26(5): 110-115. [23] 苏菲, 尚德重, 汪建波, 等. 基于陀螺仪和加速度计的帆船运动姿态测量[J]. 太赫兹科学与电子信息学报, 2014, 12(2): 183-190. [24] D. F. Hesser, K. Altun, B. Markert. Monitoring and tracking of a suspension railway based on data-driven methods applied to inertial measurements[J]. Mechanical Systems and Signal Processing, 2022, 164: 108298. DOI: 10.1016/j.ymssp.2021.108298
[25] X Wei, F Liu, L Jia. Urban rail track condition monitoring based on in-service vehicle acceleration measurements[J]. Measurement, 2016, 80: 217-228. DOI: 10.1016/j.measurement.2015.11.033
[26] 崔晓阳. 多传感器组合测姿系统设计及姿态解算算法研究[D]. 杭州: 杭州电子科技大学, 2017. [27] 李松伟, 乔书波, 马洪磊, 等. 考虑设计姿态辅助IMU/ODO的轨道不平顺检测算法[J]. 南京信息工程大学学报, 2024, 16(1): 120-127. [28] 肖克, 柏文琦, 王理, 等. 转向架滚动振动试验台在线原位校准技术研究[J]. 计量科学与技术, 2024, 68(4): 11-17. DOI: 10.12338/j.issn.2096-9015.2023.0351 [29] PENG F, XIE Q, TAO G. Multi-source onboard data-driven method for intelligent identification of subway track irregularities[J]. Journal of Central South University (Science and Technology), 2024, 55(6): 2432-2445.
[30] 李奇, 戴宝锐, 杨飞, 等. 轨道平顺性检测方法现状及发展综述[J]. 铁道学报, 2024, 46(7): 101-116. DOI: 10.3969/j.issn.1001-8360.2024.07.011
计量
- 文章访问数: 5
- HTML全文浏览量: 1
- PDF下载量: 0
