Improved Strain Field Measurement Based on SPM and DIC
-
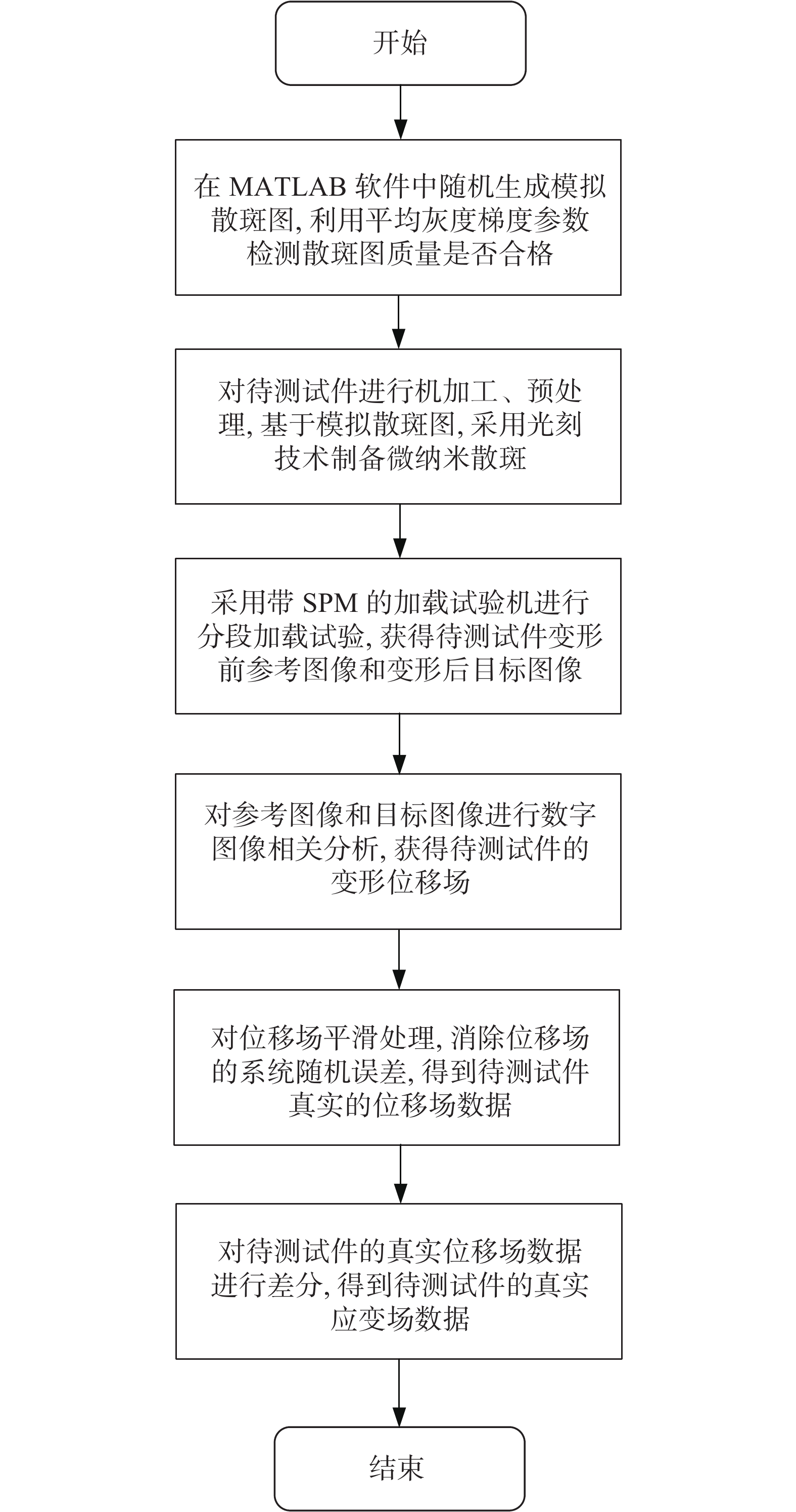
摘要: 微纳米尺度下的应力/应变测量方法是实验力学研究的重要方向之一。现有的许多研究忽略了待测试件表面的散斑图质量、系统随机误差、计算流程等因素对最终的应变场测量精度的影响。围绕基于扫描探针显微镜的数据图像相关技术实现过程,提出科学的评估准则、优化位移场计算方法。实验结果表明,所提出的应变场计算方法在精度控制方面的性能得到显著提升。Abstract: The strain field measurement on the micro/nano scale is one of the most important research topics of experimental mechanics. Most existing research ignored the influences of the speckle image quality, the systematic random error, calculation processes and other factors on the accuracy of strain field measurement. In order to overcome the above challenges, the implementation of the Digital Image Correlation (DIC) technique based on the Scanning Probe Microscope (SPM) was investigated, and scientific evaluation criteria and an improved displacement field calculation method were proposed. Experimental results showed that the estimation performance of the displacement field was significantly enhanced in terms of accuracy control.
-
Key words:
- metrology /
- strain field measurement /
- SPM /
- DIC /
- average grayscale gradient /
- micro/nano metrology
-
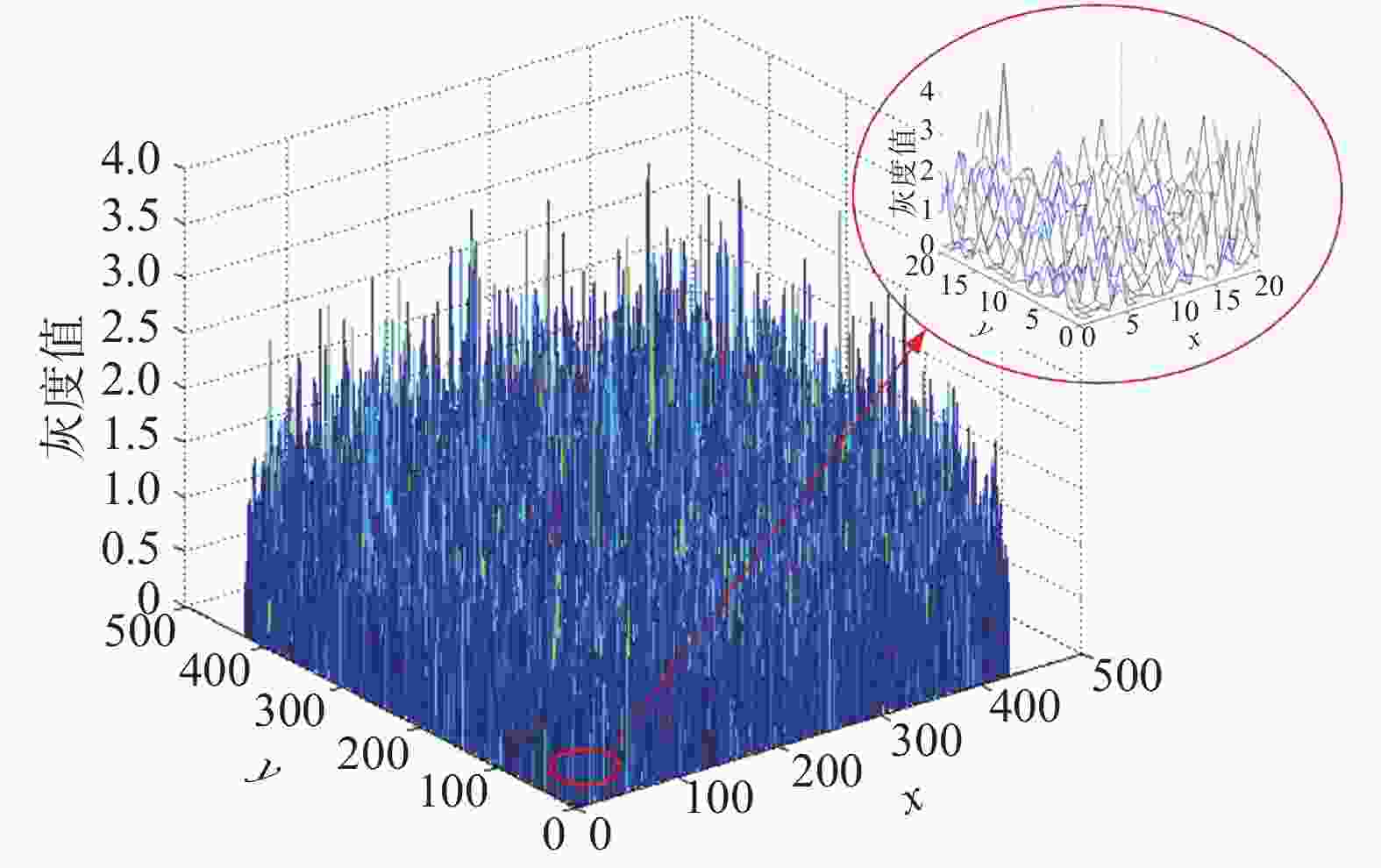
表 1 散斑图平均灰度梯度对比
Table 1. Average grayscale gradient of speckle images
选取函数 R=1 R=3 R=5 式(10) 1.86 1.86 1.88 式(11) 0.06 0.38 0.75 表 2 位移场估计误差
Table 2. Estimation error of the displacement field
变形程度 3 6 9 12 散斑区域尺寸 48 5.9% 6.5% 7.2% 3.8% 64 4.7% 6.2% 5.4% 3.4% 128 1.1% 1.3% 1.2% 1.3% -
[1] Pataky G J, Sehitoglu H. Experimental methodology for studying strain heterogeneity with microstructural data from high temperature deformation[J]. Experimental Mechanics, 2015, 55(1): 53-63. doi: 10.1007/s11340-014-9926-7 [2] Zhang J, Cai Y, Ye W, et al. On the use of the digital image correlation method for heterogeneous deformation measurement of porous solids[J]. Optics and Lasers in Engineering, 2011, 49(2): 200-209. doi: 10.1016/j.optlaseng.2010.09.015 [3] 杜亚志, 王学滨, 董伟, 等. 基于一阶及二阶DIC方法的常应变剪切带的测量误差分析[J]. 计量学报, 2018, 39(1): 66-71. doi: 10.3969/j.issn.1000-1158.2018.01.15 [4] Dong Y L, Pan B. A review of speckle pattern fabrication and assessment for digital image correlation[J]. Experimental Mechanics, 2017, 57(8): 1161-1181. doi: 10.1007/s11340-017-0283-1 [5] Nautiyal P, Zhang C, Champagne V K, et al. In-situ mechanical investigation of the deformation of splat interfaces in cold-sprayed aluminum alloy[J]. Materials Science and Engineering: A, 2018, 737: 297-309. doi: 10.1016/j.msea.2018.09.065 [6] 丁健, 罗文波, 袁宝峰, 等. 数字图像相关测量方法及其在航天器结构微变形测量中的应用[J]. 计量学报, 2017, 38(S1): 89-93. [7] Landauer A K, Patel M, Henann D L, et al. A q-factor-based digital image correlation algorithm (qDIC) for resolving finite deformations with degenerate speckle patterns[J]. Experimental Mechanics, 2018, 58(5): 815-830. doi: 10.1007/s11340-018-0377-4 [8] Bruck H A, McNeill S R, Sutton M A, et al. Digital image correlation using Newton-Raphson method of partial differential correction[J]. Experimental mechanics, 1989, 29(3): 261-267. doi: 10.1007/BF02321405 [9] Palanca M, Brugo T M, Cristofolini L. Use of digital image correlation to investigate the biomechanics of the vertebra[J]. Journal of Mechanics in Medicine and Biology, 2015, 15(2): 154-164. [10] Su Y, Zhang Q, Xu X, et al. Quality assessment of speckle patterns for DIC by consideration of both systematic errors and random errors[J]. Optics and Lasers in Engineering, 2016, 86: 132-142. doi: 10.1016/j.optlaseng.2016.05.019 [11] Yaofeng S, Pang J H L. Study of optimal subset size in digital image correlation of speckle pattern images[J]. Optics and lasers in engineering, 2007, 45(9): 967-974. doi: 10.1016/j.optlaseng.2007.01.012 [12] Zhan Q, Yuan Y, Fan X, et al. Digital image correlation involves an inverse problem: A regularization scheme based on subset size constraint[J]. Optics and Lasers in Engineering, 2016, 81: 54-62. doi: 10.1016/j.optlaseng.2016.01.007 [13] Pan B. Digital image correlation for surface deformation measurement: historical developments, recent advances and future goals[J]. Measurement Science and Technology, 2018, 29(8): 082-091. [14] Pan B, Lu Z, Xie H. Mean intensity gradient: An effective global parameter for quality assessment of the speckle patterns used in digital image correlation[J]. Optics & Lasers in Engineering, 2010, 48(4): 469-477. [15] 苏勇, 张青川. 数字图像相关的噪声导致系统误差及散斑质量评价标准[J]. 实验力学, 2017, 32(5): 699-717. [16] Pan B, Qian K, Xie H, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review[J]. Measurement Science & Technology, 2009, 20(6): 152-154. -

 作者投稿
作者投稿 专家审稿
专家审稿 编辑办公
编辑办公

 下载:
下载: